Rounding numbers is often taught in a very rule-based way, not conceptually.
"Just look at the next door neighbor and if it's 5 or higher, the number goes up. If it's 4 or less, the number goes down."
That probably sound really familiar to most adults. There are even a ton of cute sayings to help us remember this idea.
I like to focus on a couple of things when teaching rounding. Firstly, I ditch the phrase, "goes down" and replace it with "stays the same." The number in the position you're rounding never goes down. It either goes up or stays the same. This can be confusing for some. Secondly, and most importantly, we start rounding by placing numbers on a number line. This helps us determine if the number rounds up, or stays the same.
For example, if we're rounding 437,284 to the nearest hundred, we would make a number line. One end of the number line will be labeled with the hundred thousand the number is already in - 400,000. The high end of the number line will be labeled with the next hundred thousand - 500,000. Next we find the middle of the number line - 450,000. Finally we determine if the number falls to the left of 450,000 or to the right of 450,000. We do this by focusing on the ten thousands place (this is where the whole "look next door" idea originates.)

After we practiced this MANY times, rounding to MANY different places, we moved to the shortcut.
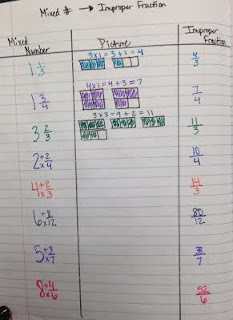
 The next day, we talked
about how we went between the two types of fractions using pictures to
help us. After examining our pictures, we noticed some shortcuts to help
us be more efficient when changing from one type of fraction to the
other. Eventually, the kids discovered the multiplication and division
connection to help speed them along.
The next day, we talked
about how we went between the two types of fractions using pictures to
help us. After examining our pictures, we noticed some shortcuts to help
us be more efficient when changing from one type of fraction to the
other. Eventually, the kids discovered the multiplication and division
connection to help speed them along.