Breaking Apart Numbers in Multiplication

A student's list of combinations she's still working on

Breaking apart a number using arrays as a visual

Breaking apart a number using arrays as a visual

What we did this week was go through our basic facts and determine which ones we know quickly, and the ones with which we still need some practice. We made a list of those we're still working on, and came up with ways to "get" to that answer. For example, if 12 x 9 is still a struggle, we could think of it as (12 x 6) + (12 x 3). We made the arrays to go with the problem, which made visualizing the strategy a little easier.

If a student can visualize breaking apart a number for basic multiplication, it's going to make his life much easier when we get to 2-digit by 2-digit multiplication. It's so important for the kids to understand the place value involved in larger multiplication, and learn to make their numbers work for them. Flexibility with numbers is a HUGE concept to grasp, and it has arguably the greatest impact on the success of a mathematician!!!!!!

Divisibility Rules

Just a few divisibility rules

This week we listed out multiples of many numbers, and used these lists to help us come up with some divisibility rules. We thought knowing these rules might help us when determining factors of a number. We spread this process out over a couple of days, as it can be a bit overwhelming all at once! We made some great connections!!!

Making Arrays

Our introduction into finding all possible arrays

An example of our T-Chart to help keep us organized

As we continued our discussion on arrays, we tried to come up with a way to determine if we'd found all the possible arrays for a number. First we talked about what those arrays are actually modeling (factors). Then we came up with our T-Chart to list out the factor pairs in an organized way. We can determine we're done when we begin repeating numbers. All this discussion is leading up to 2x2 multiplication.

More Density

View of our jars from the top

A fuzzy side view of our jars.

As we continued our exploration of density, we began another investigation using three jars of unknown liquids. The kids didn't know the contents of the jars until after the investigation was completed. Jar #1 contained 60 mL of dish soap (blue liquid). Jar #2 contained 60 mL of baby oil. Jar #3 was nothing but air, which is why I covered it in foil. I didn't want to spoil the surprise. Some kids knew right away there was nothing in it, but some were convinced I had put something in there! The groups all measured the mass of each jar using the triple beam balance. Then they added the jars to the tub of water to observe which was the most dense/least dense. All groups came to the conclusion the blue liquid had the most mass and was the and most dense, while the foil-covered jar had the least amount of mass and was the least dense.

We then discussed why it was so important both the liquids have the same volume. If the volumes are different, we wouldn't know if the blue liquid was, in fact, more dense, or if there was just more liquid in the jar.

Arrays

Arrays

Yesterday we began discussing arrays. This will eventually lead us into bigger multiplication. We just discussed what an array looks like (equal rows and columns), the dimensions, and how we find the number of objects in the array without counting each one individually.

This is never a hard concept for the kids to grasp. Usually the only challenge they have is forgetting to count "Mr. Popular." This is what I call that little guy in corner. We have to remember he's super popular, and both the rows and the columns want him in their groups. So he must be counted with the rows, and with the columns! 

Our Arrays Anchor Chart

Adding and Subtracting Money

Adding and Subtracting Money

This is our journal entry for adding and subtracting money. It was basically just a run-though of all our addition and subtraction strategies, but I threw in money instead of just whole numbers. Lots of discussion along the way!

Subtraction Strategies

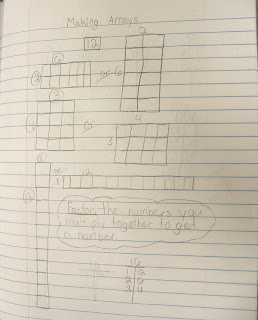
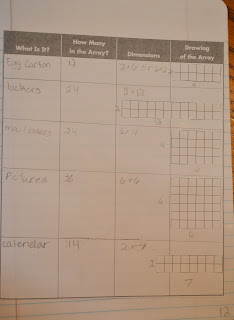
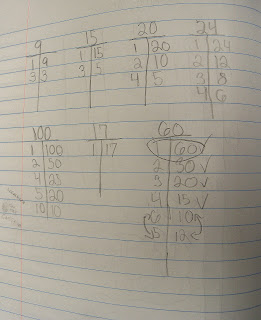Student Journal - Subtraction Strategies

As a class, we discussed different subtraction strategies. The strategy most of our kids are familiar with (at least if they've been in the district a while) is the number line. If the problem were 634-319, they would start their number line at 319, and count on by taking "jumps" until they reached 634. Then they add up their jumps, and there's the difference. It's like subtraction without subtracting!! For those kiddos who struggle with subtraction, this strategy is perfect until they're more comfortable!

The second strategy we discussed is subtracting by place value. With subtraction (unlike adding by place value) it's very important to only break up one number by place value. Otherwise, you're looking at major confusion for most kids. If we were to solve 634-319 again, we would start with 634-300 = 334, then 334-10=324, then finally 324-9=315.

Of course one of our strategies is vertical subtraction, which is my absolute LEAST favorite way for kids to subtract - at least until they have a major grasp on place value! For me to allow a child to subtract vertically, he/she must explain to me step-by-step how to do it, all the while talking in terms of place value, not numbers. For example, 634-319 would be explained something like this:

"I cannot take 9 from 4, so I borrow a group of 10 from the 30 so it now becomes 20. The 4 now becomes a 14. 14 minus 9 is 5. 20 minus 10 is 10, but I only write the 1 because I'm working in the tens place. 600 minus 300 is 300, so my answer is 315."

I know that may not sound too difficult, but when the numbers get bigger and there's more borrowing involved, it's gets pretty confusing. If they can explain the process to me in a way that shows me they know what they're doing and why they're doing it, they're free to do vertical subtraction all day long!

Our last strategy is shifting up/shifting down. I presented this strategy as a super-secret strategy that only they know. We even closed the blinds and door. Ha ha!! This strategy is for those kiddos who need the organization of the vertical strategy, but are still struggling with borrowing. We started by marking 8 and 16 on our number line and subtracting for a difference of 8. Then I added 1 to each number, making 9 and 17. Looking at our number line, we discovered it still had a difference of 8. Then I subtracted 3 from each number, making 5 and 13. Again, still a difference of 8. This led us into the discussion that if you change both numbers in the same way, you're not changing the difference between them. So we concluded that sometimes shifting the numbers up or down might help us in subtraction. For example, if I had the problem 2,002-412, I could shift both my numbers down 3, leaving me with 1,999-409. This is a much friendlier number to subtract! We did lots of examples using this strategy! Then we spent a little while coming up with reasons why this strategy wouldn't work the same for addition!! :)

Our Subtraction Strategies Anchor Chart

Another Subtraction Strategy

Addition Strategies

Addition Strategies

After our "How Many Miles to 1,000?" lesson in which we discussed new ways to solve our problems, we decided to add an addition strategies page. We focused on three main addition strategies.

#1 is adding by place value. Some of the kids call it decomposing the number, which is perfectly fabulous. This is basically just adding a place at a time. What makes this way so great, is that it focuses on adding the value of each place, instead of just the number in the place. For example, 235 + 316 could be broken up into 200 + 300, 30 + 10, and 5 + 6. Once you add those parts together, you add their sums for your answer. I know this looks a little long to those of us who were taught the traditional algorithm. While it does involve more steps, it really helps the kids see the value of what they're adding. When carrying, they understand it's a group of 10, not a 1.

The second way is by adding-on using a number line. You begin with your first number, then add on the second number in whatever number chunks you wish. Begin at 235, then add 300 to get you to 535. Then add 10 to get you to 545. Finally, add 6 to get you to 551. We're basically just breaking up that 316 into smaller, easier-to-add-mentally, chunks. I love this way of adding because the kids can customize it for their own skill level. If they need smaller chunks, they can add small numbers. If they see those bigger jumps, they can do that as well. This way really helps the kids make their numbers work for them, which will lead to stronger mental math.

The last way is the typical vertical algorithm. I've warned my kids that if they choose vertical, which is fine, they'd better be able to explain what all the numbers they've carried mean! No carrying a 1! It's a group of 10!

Our Addition Strategies Anchor Chart

The Scientific Method

The Scientific Method

On Friday we discussed the Scientific Method, and what each step looks like. The first step is determining the question/problem. We brainstormed ways to make a testable question - one we can design and conduct an experiment to answer, which leaves no room for opinions. For example, we wouldn't come up with the question, "A paper airplane made out of which type of paper is the best?" The students helped me figure out why this could lead to many different answers. I could look at the best one as the one that turned out the prettiest, while someone else would see the best one as being the one that flew the farthest. The wording of the question is very important!

The second step is drawing from our background knowledge. Sometimes this might require a little research beforehand. For example, if I were to do an experiment involving any type of car part, I would certainly need to do some research before coming up with my hypothesis!

The third step is formulating our hypothesis based on our background knowledge or research. Step four testing our hypothesis. This involves deciding on our ONE variable, and many constants. The kids and I brainstormed why it is so important to only change one variable at a time! Step five is analyzing our data to draw our conclusion, which could include retesting (maybe even many times!) for reliability.  Finally, the sixth step is to report our findings. You may not know this, but a standard for our 4th graders is to "communicate valid, oral, and written results supported by data." This is a very important step!  

How Many Miles to 1,000?

A great example of a student's entry

My journal from the lesson

Today I posed this question to your kiddos: You're going on a trip 1,000 miles away. You've already gone 632 miles, so how could you figure out how many miles are remaining? That's all the instruction I gave. I like this approach because it gives a real-life scenario and lets the kids really think about what strategy makes sense! We had LOTS of difference strategies, from number lines, to adding or subtracting by place value, to vertical subtraction. It's so important the kids understand the concept of subtraction, and how they can use addition to accomplish the same goal if they just change their ways of thinking. The kids had an opportunity to explain their method to the others. I heard lots of, "Oh! I get what he did!" That makes my heart so happy! We then solved a similar problem, but this time they had only traveled 419 miles. I challenged them to use a different strategy to solve this problem than they did for the original problem.