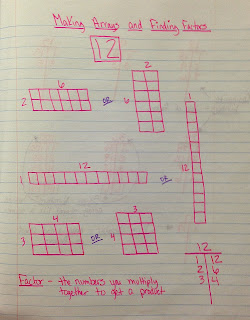This week we took a brief look at fractions. We started by reviewing what we already know about fractions such as definitions and pictures.
Friday, October 28, 2016
Fraction Review and Intro to Improper Fractions
Posted by Rebecca May at 11:55 AM 0 comments
Labels: 4th grade, Fractions, Improper Fractions
Monday, October 24, 2016
Moving to the Standard Multiplication Algorithm
  |
| The progression from matrix box to standard algorithm |
Posted by Rebecca May at 8:08 AM 0 comments
Labels: 4th grade, math, multiplication
Wednesday, October 19, 2016
Multiplication Area Model
We finally got to begin 2-digit by 2-digit multiplication this week! I began by reviewing with them the area model we used when multiplying by 1 digit. Then the kids self-discovered (with my prompting and questioning) that they could create an area model for 2x2 multiplication. They referred to it as the "double-decker couch." Ha! The
kids are absolutely loving the 2x2 area model!! They love it because it's super easy. I love is because
it shows them the place value involved in 2x2 multiplication. They can
actually see the process of multiplying the ones and tens of one number
by the ones and tens of the second number. When they finally move to
vertical multiplication, they'll actually understand why it works! There's nothing better than actually understanding
WHY you do something!!!
The area model can actually be
formatted to fit more than 2x2 multiplication. We played around with differently-sized numbers and made our matrix box fit those problems as well.
 |
| Our class anchor chart |
 |
| Close-up of the box itself |
 |
| An example |
Posted by Rebecca May at 7:04 AM 0 comments
Labels: 4th grade, multiplication
Friday, October 14, 2016
Breaking Apart Multiplication
As we move to multiplying larger numbers, I like to guide them into the algorithm. We start by investigating the pattern when multiplying by multiples of 10. We look at the problems 2 x 3 = 6, 2 x 30 =60, and 2 x 300 = 600. We discuss what is the same/different about each problem, then we look at several other similar examples. Eventually the kids see the pattern of just "adding a zero" each time. Patterns are a great shortcut, but it's important the kids understand why they work.
Next we move to breaking apart larger multiplication problems, such as 18 x 5. We can break the 18 into 10 and 8 to help us multiply easier.
This will lead us into the multiplication algorithm next week.
Posted by Rebecca May at 8:46 AM 0 comments
Labels: 4th grade, math, multiplication
Monday, October 10, 2016
Finding the Factors of 12
But how can we keep our factors organized so we can make sure we've found all the factors? This leads us to making our T-Chart. We always start with 1 and the number itself. Then we move to the next number in the number line, 2. We know 2 is a factor because 12 is even, so we then find the partner for 2 which is 6. Then we move to 3, which has a partner of 4. The next number in the number line is 4, which we've already used, so we know we're done. Once numbers start to repeat, we've found all our factors. This lesson is followed by lots of practice finding the factors of many different numbers. As we're making our factor lists, we discuss the definition of prime, composite, and square numbers.
Posted by Rebecca May at 6:50 AM 0 comments
Labels: 4th grade, Arrays, Factors, multiplication
Thursday, October 6, 2016
Elapsed Time
Posted by Rebecca May at 9:58 AM 0 comments
Labels: 4th grade, Elapsed Time, math, time